What is Benford's Law?
Benford's Law, or the First-Digit Law, posits that in many naturally occurring collections of numbers, the leading digit is likely to be small. For instance, the number 1 appears as the first digit about 30% of the time, while higher numbers like 9 appear as the first digit less frequently, around 5% of the time. This counterintuitive phenomenon applies across various domains, from financial accounts to street addresses.
The Experiment
The dataset in focus was a collection of supermarket sales figures. To analyze this data, I decided to use Benford's Law as a litmus test for the numbers' authenticity. The hypothesis was simple: if the sales data conformed closely to Benford's distribution, it would likely be legitimate. However, a significant deviation could hint at manipulation or anomalies.
Handling Numbers Below 1
A unique challenge arose when dealing with numbers smaller than 1. These numbers, such as 0.876, initially led to a '0' as their leading digit, which is not covered in Benford's Law. This presented a problem: how do you apply a law based on leading digits starting from 1 to 9 to numbers that apparently start with 0?
Solution:
I devised a method to extract the first non-zero digit from these numbers. Here's a snippet of the Python code that made it possible:
def extract_leading_digit(num):
num = abs(num) # Handle negative numbers
while num < 1 and num != 0:
num *= 10
return int(str(num)[0])
df['leading_digit'] = df['sales_column'].apply(extract_leading_digit)
Analysis and Results
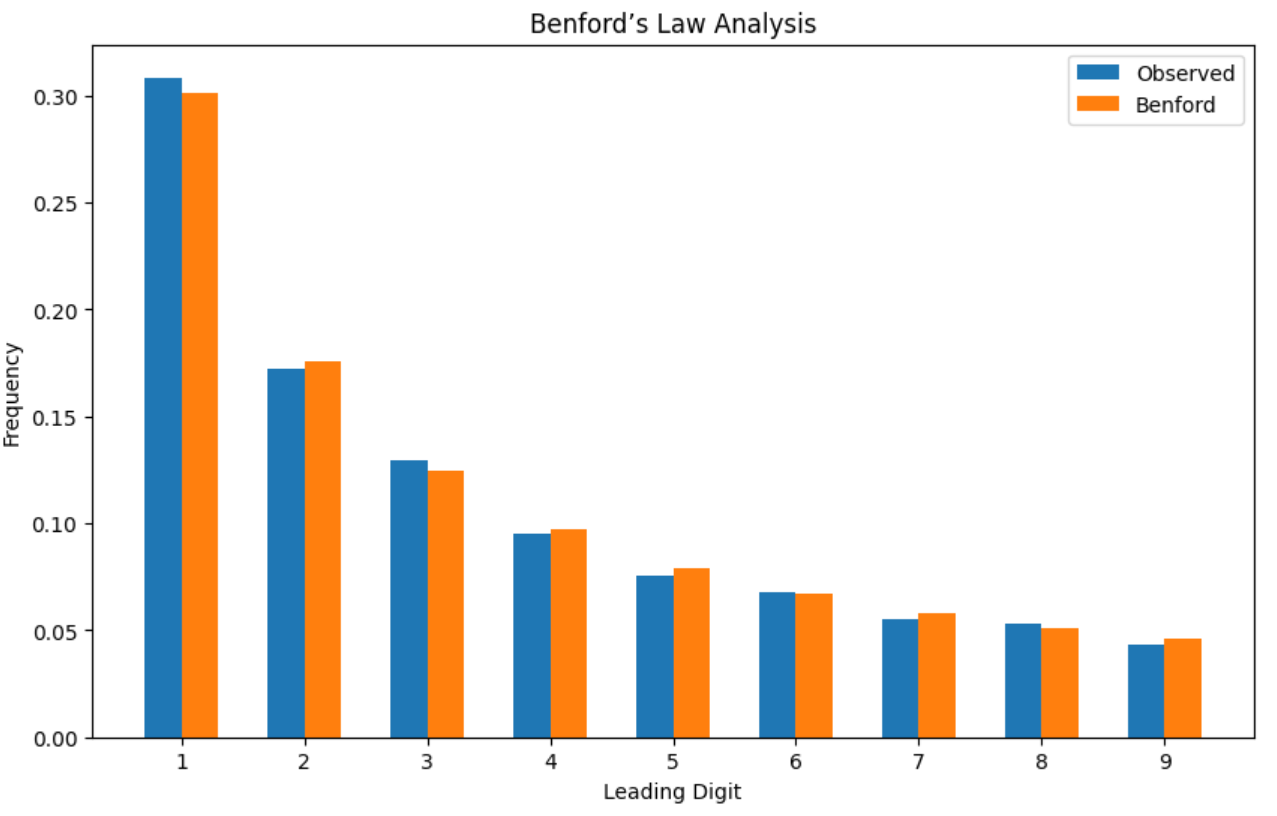
Once every number had a valid leading digit, I compared their distribution against the expected frequencies from Benford's Law:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Expected frequencies based on Benford's Law
expected_frequencies = np.log10(1 + 1/np.arange(1, 10))
# Observed frequencies in the dataset
observed_frequencies = df['leading_digit'].value_counts(normalize=True)
observed_frequencies = observed_frequencies.reindex(np.arange(1, 10), fill_value=0)
# Plotting
plt.figure(figsize=(10, 6))
plt.bar(np.arange(1, 10) - 0.15, observed_frequencies, width=0.3, label='Observed')
plt.bar(np.arange(1, 10) + 0.15, expected_frequencies, width=0.3, label='Benford')
plt.xticks(np.arange(1, 10))
plt.xlabel('Leading Digit')
plt.ylabel('Frequency')
plt.legend()
plt.title("Benford's Law Analysis of Supermarket Sales Data")
plt.show()
The sales data showed a remarkable alignment with Benford's Law, suggesting the figures were likely genuine and free from overt manipulation.
Conclusion
This experiment was a profound reminder of the power of statistical analysis in validating and understanding real-world data. By adapting methods to handle specific data characteristics (like numbers below 1) and using Benford's Law, we can uncover deeper insights and ensure data integrity. It's a testament to the synergy between mathematics and the ever-evolving world of data.

